
Did you know there is a common element in much, if not most, of what we as humans consider beautiful? That beauty isn’t entirely subjective? This element is why some things are considered beautiful for ages, even though trends have changed. The ancient Greeks said that all beauty boils down to mathematics. Mathematicians, biologists, philosophers, and sociologists have all searched for a shared “something” which might explain our perception of beauty. Scientists have proven people are attracted to symmetrical patterns, though symmetry alone cannot explain why people find some things beautiful and other things less so.
It turns out the Greeks were right about the connections of beauty and mathematics. The element is a ratio of 1:1.618. This is known as the Golden Ratio. The sequence is also known as the Fibonacci numbers or the Fibonacci Sequence, after its discoverer Leonardo Pisano, also known as Fibonacci. Fibonacci discovered it around the year 1202.
Fibonacci
In his book he introduced his famous rabbit problem: “A certain man put a pair of rabbits in a place surrounded by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair from which the second month on becomes productive?” (Liber Abaci).
His solution led to a series of numbers. The first two numbers are 0 and 1, and each following number is the sum of the two numbers before it: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…. The individual numbers within this sequence are called Fibonacci numbers. The Fibonacci sequence can also be expressed using this equation: Fn = F(n-1) + F(n-2), where n is greater than 1 (n>1).
This sequence doesn’t seem like much unless you divide each number by the one which comes before it, e.g., 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13. The answers for these examples are 1.000, 2.000, 1.500, 1.667, 1.625, and 1.615. As Fibonacci numbers get bigger, the ratio between each pair of numbers gets closer to 1.61833988749895 (Phi/Φ). Phi is the Golden Ratio.
This ratio can also be found using two quantities, like the lengths of two line segments. Two quantities have the Golden Ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. This can be written as long segment ÷ short segment = line segment ÷ long segment=
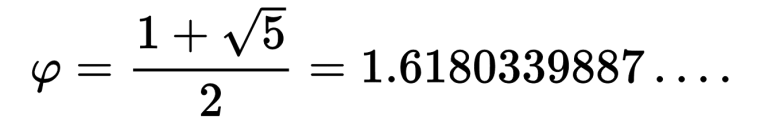
Golden Rectangle
A Golden Rectangle works in a similar way, as it’s a rectangle with a long side of a+b and a short side of a. If you cut off a square section so each side is of equal length to the shortest side, the piece that remains has the same ratio of side lengths as the original rectangle. Thus, the ratio between sides a and b is Φ or 1.618…, seen in this equation:
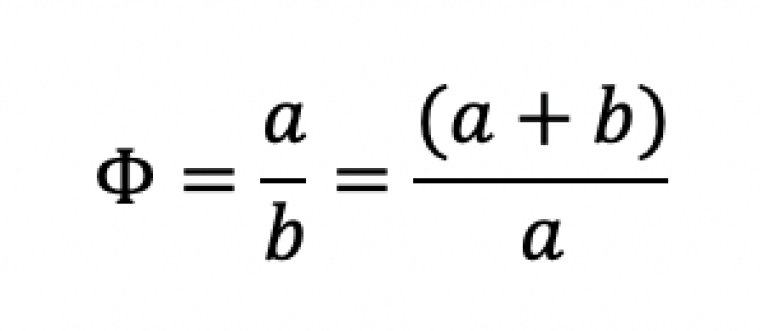
You can increase this pattern by adding a larger square to the long side (a+b) of a rectangle. Then you can do the same thing to the rectangle that results from that combination.
By adding a line that forms a quarter circle in each square the lines connect to form a spiral. The Golden Ratio can be used with other shapes too.
Animals
In nature, it can be found in all sorts of things, including animals and plants. Among animals it’s found on the curled tentacles of the octopus and the horns of rams. Dolphins, starfish, sand dollars, sea urchins, ants, and honey bees all have a measurement from the navel (or nearest equivalent) to the ground, and the top of their heads to their navels is equal to the ratio.
The reproduction characteristics, and the way some birds swoop to catch prey are all directly related to Fibonacci numbers.
Plants
The Golden Ratio is also found in plants. For example, in flowers the petal counts are all numbers of the Fibonacci pattern. You can also see this when a flower has multiple layers of petals. Each layer increases the petal count in sync in sync with Fibonacci numbers.
The seed patterns in flowers tend to follow these same patterns; when they spiral, they almost always follow the spiral pattern explained above. Examples include sunflower seed-heads, and pinecones. The patterns of cauliflower heads and pineapple skins follow the Fibonacci numbers.
Generally, the pattern of trees’ root systems and branches which grow from their trunks follows the Fibonacci pattern almost exactly.
The Golden Ratio can also be found in the spiral of hurricanes and cyclones, and the spiral of galaxies.
Us
Most significantly, it is found on us. It's found on our faces and our fingerprints. While we each have a unique fingerprint, the arcs in our prints follow along the Fibonacci arc of the spiral. Is it any wonder then that we use it as a blueprint for all art, design, architecture, and other creative pursuits? If you’re like me, you probably had no idea how often the Fibonacci pattern could be found in the natural world.
Looking at the world, I think it’s safe to say the Golden Ratio is God’s signature, demonstrating clearly His order and design. As it says in Scripture” “How great are Your works, O LORD! Your thoughts are very deep!” (Psalm 92, verse 5).

Katelin Staples is from Gladstone, Queensland. By day Katelin is employed as a proofreader. Katelin has a passion for discovering the deep things of God and how they affect the world around us.